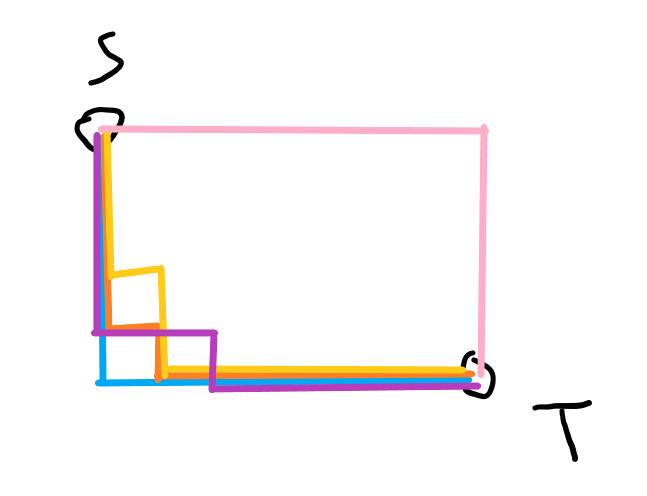紫名后第一次没跑路的场，好像黄了

熬夜等分，成功了，感觉还是挺快乐的

1358A Park Lighting

一个点最多照两个，而且一定能组合，除非总数是奇数，会多用一个。

a.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <bits/stdc++.h>
using namespace std;

int main() {
    int q;
    cin >> q;
    while (q--) {
        int a, b;
        cin >> a >> b;
        a *= b;
        if (a & 1) cout << a / 2 + 1 << endl;
        else cout << a / 2 << endl;
    }
    return 0;
}

1358B Maria Breaks the Self-isolation

按要求的从小到大排序，每次检测当前的大妈要求是否可行，一次打电话全叫来。

b.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>
using namespace std;
typedef vector<int> vi;

int main() {
    int q;
    cin >> q;
    while (q--) {
        int n;
        cin >> n;
        vi a(n);
        for (int &i : a) cin >> i;
        sort(a.begin(), a.end());
        int ans = 1;
        for (int i = 0; i < n; ++i) {
            if (i + 1 >= a[i])
                ans = i + 2;
        }
        cout << ans << endl;
    }
    return 0;
}

1358C Celex Update

首先可以想到，最大值是蓝色路径，最小值是粉色路径。那么比最大值小 $1$ 的就是橙色路径，再小 $1$ 的就是黄色和紫色路径了，那么可以想到只有 $(x_2-x_1)\times (y_2-y_1)+1$中取值。

c.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

int main() {
    int q;
    cin >> q;
    while (q--) {
        ll x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        y2 -= y1; x2 -= x1;
        cout << x2 * y2 + 1 << endl;
    }
    return 0;
}

1358D The Best Vacation

可以想到 $x=1$ 时一定是要取最大的$d_i$，$x=2$ 时再取 $d_i-1$，依次类推，那么答案的有边界一定会在某个月的最后一天了。
有了这个发现，就可以进行双指针，注意年可以循环以及维护权值就可以了。

d.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

int main() {
    auto calc = [](ll x) { return (1 + x) * x / 2; };

    int n;
    ll x;
    cin >> n >> x;
    vector<int> d(n * 2 + 1);
    for (int i = 1; i <= n; ++i) {
        cin >> d[i];
        d[i + n] = d[i];
    }
    n *= 2;
    ll tx = 0, ans = 0, a = 0, b = 1, tmp = 0;
    for (int i = 1; i <= n; ++i) {
        tx += d[i];
        tmp += calc(d[i]);
        while (tx > x) {
            ll t = min(tx - x, d[b] - a);
            tx -= t;
            tmp -= calc(t + a) - calc(a);
            a += t;
            if (a == d[b]) {
                ++b;
                a = 0;
            }
        }
        ans = max(ans, tmp);
    }
    cout << ans << endl;
    return 0;
}

1358E Are You Fired?

首先按分类讨论下：

  • $x>0$，如果 $n$ 个数求和是整数，那么直接汇报，此时 $k=n$。
  • 否则，$k >= \lceil \frac {n}{2} \rceil + 1$，首先想到枚举最右的 $i（n-k+1$，也就是枚举 $k$），然后我们从右向左判断后缀和 $suf[i] - suf[i+k] > 0$ 是否均成立，这一步由于回溯是 $n^2$ 的；

然而又可以想到，如果对于 $j$ 有 $suf[i] - suf[i+k] < 0$ 不成立，那么对于更大的 $k$，都会是使式不成立，因此下一次枚举直接从 $j-1$ 继续即可，那么每个位置只会访问一遍，不需要回溯，$O(n)$。

e.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

int main() {
    int n;
    cin >> n;
    vector<ll> a(n + 5), sum(n + 5);
    ll x, t = 0;
    int m = (n + 1) / 2;
    for (int i = 1; i <= m; ++i) {
        cin >> a[i];
        t += a[i];
    }
    cin >> x;
    if (x > 0) {
        if (t + x * (n / 2) > 0) {
            cout << n << endl;
            return 0;
        } else {
            cout << -1 << endl;
            return 0;
        }
    }

    for (int i = n; i >= 0; --i) {
        if (i > m) a[i] = x;
        sum[i] = sum[i + 1] + a[i];
    }
    int ans = -1;
    for (int i = m, j; i >= 0; --i) {
        if (sum[i] > 0) {
            int f = 1;
            for (j = i - 1; j > 0; --j) {
                if (sum[j] - sum[j + n - i + 1] <= 0) {
                    f = 0;
                    break;
                }
            }
            if (f == 1) {
                ans = n - i + 1;
                break;;
            }
            i = j;
        }
    }
    cout << ans << endl;
    return 0;
}