没啥难度，和上次55开（除了我僵硬的一p）

Bike Tour

Bike Tour.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <bits/stdc++.h>
using namespace std;

int main() {
    int T;
    cin >> T;
    for (int cas = 1; cas <= T; ++cas) {
        int n;
        cin >> n;
        vector<int> a(n);
        for (int &i : a) cin >> i;
        int ans = 0;
        for (int i = 1; i < n - 1; ++i) {
            if (a[i] > a[i - 1] && a[i] > a[i + 1]) ++ans;
        }
        cout << ans << endl;
    }
    return 0;
}

Bus Rountes

Bus Rountes.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

int main() {
    int T;
    cin >> T;
    for (int cas = 1; cas <= T; ++cas) {
        int n; ll d;
        cin >> n >> d;
        vector<ll> a(n);
        for (ll &i : a) cin >> i;
        ll las = d;
        for (int i = n - 1; i >= 0; --i) {
            las = las / a[i] * a[i];
        }
        ll ans = las;
        cout << "Case #" << cas << ": " << ans << endl;
    }
    return 0;
}

Robot Path Decoding

差不多就是模拟叭，就是加（）可以当作递归写，反正数据范围很小，统计贡献方便且快。

Robot Path Decoding.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll, ll> pll;

pll go(string &s, int l, int r, int mul) {
    pll res;
    for (int i = l; i <= r; ++i) {
        if (isdigit(s[i])) {
            int cnt = 0;
            for (int j = i + 1; j <= r; ++j) {
                if (s[j] == '(') ++cnt;
                if (s[j] == ')') --cnt;
                if (cnt == 0) {
                    pll t = go(s, i + 1, j, s[i] - '0');
                    i = j;
                    res.first += t.first;
                    res.second += t.second;
                    break;
                }
            }
        }
        if (s[i] == 'N') res.first += mod - 1;
        else if (s[i] == 'S') res.first += 1;
        else if (s[i] == 'E') res.second += 1;
        else if (s[i] == 'W') res.second += mod - 1;
        if (res.first > mod) res.first %= mod;
        if (res.second > mod) res.second %= mod;
    }
    res.first = res.first * mul;
    res.second = res.second * mul;
    if (res.first > mod) res.first %= mod;
    if (res.second > mod) res.second %= mod;
    return res;
}

int main() {
    int T;
    cin >> T;
    string s;
    for (int cas = 1; cas <= T; ++cas) {
        cin >> s;
        pii ans = go(s, 0, s.length() - 1, 1);
        ans.first++; ans.second++;
        if (ans.first > mod) ans.first %= mod;
        if (ans.second > mod) ans.second %= mod;
        printf("Case #%d: %d %d\n", cas, ans.second, ans.first);
    }
    return 0;
}

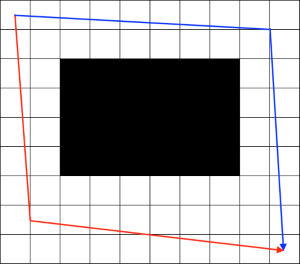
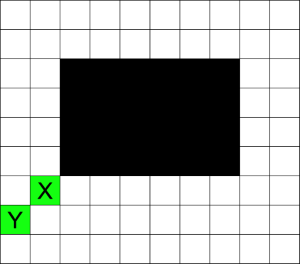
Wandering Robot

看了题解分析后，感觉写了这么久题，反而把计算机最原始的数值计算的功能忽略了，所以被精度问题绝杀。

分析一下可以想到假设每个格子都能走的话，走到位于$(x,y)$的概率斜着看是二项式系数除$2^n$，所以问题就变成求一些格子上$\frac{C_n^k}{2^n}$的和。

由于如上图有两条路能走，可以翻转后等效，因此下面考虑一条路。

由于求$\frac{C_n^k}{2^n}$中间太大，可以把换成$e^{\ln{\frac{C_n^k}{2^n}}} = e^{\ln{n!}-\ln{k!}-\ln{(n-k)!}-\ln{2^n}}$，预处理一下，就可以算了。
不过，由于右和下边界和内部规则不同，计算略有不同。假设当我们走到$(w,i)$时，这里上式算出来的值和实际是不同的，实际它差的是$i\in [1,i)$的和除$2$，原因还是很好想到的。

Wandering Robot.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;

double ln_fac[N], p[N];

double calc(int k, int n) {
    return exp(ln_fac[n] - ln_fac[k] - ln_fac[n - k] - p[n]);
}

int main() {
    p[1] = log(2);
    for (int i = 2; i < N; ++i) {
        ln_fac[i] = ln_fac[i - 1] + log(i);
        p[i] = p[i - 1] + p[1];
    }
    int T;
    cin >> T;
    for (int cas = 1; cas <= T; ++cas) {
        int x, y, x1, y1, x2, y2;
        cin >> x >> y >> x1 >> y1 >> x2 >> y2;
        --x, --y, --x1, --y1, --x2, --y2;
        double ans = 0;
        auto go = [&]() {
            int tx = x2, ty = y1;
            if (x2 < x) {
                double fl = 1;
                while (ty) {
                    ty--, tx++;
                    if (tx > x) {
                        fl = 0.5;
                        --tx;
                    }
                    ans += fl * calc(tx, ty + tx);
                }
            }
        };
        go();
        swap(x, y); swap(x1, y1); swap(x2, y2);
        go();
        printf("Case #%d: %.7lf\n", cas, ans);
    }
    return 0;
}